Question

In parallelogram ABCD , diagonals AC ? ? ? ? ? and BD ? ? ? ? ? intersect at point E, AE= x 2 ?16 , and CE=6x . What is AC ? Enter your answer in the box.

Answer 1

I just took the test and got the answer AC=96.

Answer 2

Length of AC = 48 units.

Explanation:

Given in parallelogram ABCD , diagonals AC and B intersects at a point E.

Length of AE =
`x^2-16` units and CE = 6x.

We have to find the length of AC.

According to the property of parallelogram:

Diagonals are intersecting each other at their midpoint.

Since, E is the midpoint AC ;

so, AE = CE

`x^2-16` =6x

or we can write this as;

`x^2-6x-16`=0

`x^2-8x+2x-16`=0

`x(x-8)+2(x-8)`=0

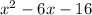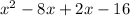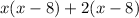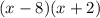`(x-8)(x+2)` = 0

Zero product property states that if ab = 0 , then either a=0 or b =0.

By zero product property, we have;

(x-8) = 0 and (x+2) = 0

x = 8 and x = -2

Since, length x cannot be negative so we ignore x = -2.

then;

x = 8

AC =
`x^2-16` =
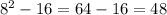`8^2 -16 = 64- 16 =48` units.

Therefore, the length of AC = 48 units.