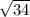Question

1. Write the expression in simplified radical form. Show your work.

3-2 square root 11/ 2+ square root 11


2. Solve the equation. Show your check then write the solution set.
x - 1 = square root 6x + 10


Score for Question 3: ___ of 6 points)
3. Given the complex number, 5 − 3i:
(a) Graph the complex number in the complex plane.
(b) Calculate the modulus. When necessary, round to the tenths place.
Answer:

Answer 1

1) 3

2) {x = 9 or x = -1}

3) (b) The modulus of the complex number 5-3i is
`√(34)`

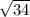
Explanation:

Problem 1

3 - 2
`(√(11) )/(2) + √(11)`

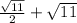
i) Cancelling out the 2's from the top and bottom of the middle term, we get

3 -
`√(11) + √(11)`

ii) Cancelling out -
`√(11)` and +
`√(11)`, we get

3 as the simplified form

Problem 2

x-1 =
`√(6x+10)`

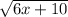
Our first goal is to get rid off the radical on the right side

i) Squaring both sides, we get

`(x-1)^(2)`=
`(√(6x+10))^(2)`

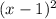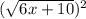
ii) (x-1)*(x-1) = 6x+10

iii) Applying the distributive property (a+b)(c+d) = ac+ad+bc+bd to the left side of the equation, we get

(x)(x)+(x)(-1)+(-1)(x)+(-1)(-1) = 6x+10

=>
`x^(2)`-x-x+1 = 6x+10

=>
`x^(2)`-2x+1 = 6x+10

iv) Subtract 6x from both sides, we get

`x^(2)`-2x+1-6x = 6x+10-6x

v) Cancelling out 6x and -6x from the right side, we get

`x^(2)`-2x-6x+1 = 10

=>
`x^(2)`-8x+1 = 10

vi) Subtracting 10 from both the sides, we get

`x^(2)`-8x+1-10 = 10-10

vii) Cancelling out 10 and 10 from the right side, we have

`x^(2)`-8x-10+1 = 0

=> 1
`x^(2)`-8x-9 = 0

viii) Coefficient of the first term = 1

Multiplying the coefficient of the first term and the last term, we get

1*(-9) = -9

We need to find out two such factors of -9 which when added should give the middle term -8

So, -9 and +1 are the two factors of -9 which when added gives us the middle term -8

ix) Rewriting the middle term, we get

`x^(2)`-9x+x-9 = 0

x) Factoring out x from the first two terms and factoring out 1 from the last two terms, we get

x(x-9)+1(x-9)=0

xi) Factoring out x-9 from both the terms, we get

(x-9)(x+1)=0

xii) Either x-9=0 or x+1=0

xiii) Solving x-9=0, we get x=9

xiv) Solving x+1=0, we get x= -1

So, solution set {x = 9 or x = -1}

Problem 3

5 − 3i

a) In order to graph the complex number 5-3i, we need to move right by 5 units on the real axis and then move down by 3 units on the imaginary axis.

See figure attached

b) A complex number is in the form of z= a+ bi

i) Comparing 5-3i with a+bi, we get a=5 and b = -3

The modulus is given by

|z| =
`\sqrt{a^(2)+b^(2) }`

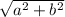
ii) Plugging in a=5 and b=-3, we get

|z| =
`\sqrt{5^(2)+(-3)^(2) }`

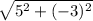
iii) |z| =
`√(25+9)`

iv) |z| =
`√(34)`

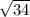
The modulus of the complex number 5-3i is
`√(34)`