Question

Find the length of arc shown in red.

Answer 1

10.99 ≈ 11cm

Explanation:

To find the length of the arc, first we need to find the circumference of the circle, which we find with the following formula :

`c=2\pi r`

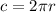
where
`r` is the radius which is indicated in the image:
`r=14cm`.

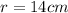so the circumference is:

`c=2\pi(14cm)\\c=87.96cm`

This is the measure of the entire perimeter of the circle, it is the measure of the 360 ° arc.

Because we only want 45 ° of those 360 °, we divide the value of the circumference by 360 and multiply po 45:

`(87.96cm(45))/(360)=(3958.2)/(360)=10.99cm`

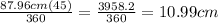
which can be rounded to 11cm

The length of the arc is 11cm

Answer 2

≈10.99525 cm.

Explanation:

1. The length of the circle is L=2πr, where π≈3.1415 and r- radius of the circle.

2. if the given arc is 45° and full circle is 360°, then the length of the arc is 45/360=0.125 of full circle, that is L(arc)=0.125L=0.25πr; ⇒ L(arc)≈0.25*3.1415*14=10.99525 (cm).