Question

Match the following reasons with the statement givem

Answer 1

AAS(Angle-Angle-Side) postulate states that if two angles and the non-included side one triangle are congruent to two angles and the non-included side of another triangle, then the two triangles are congruent

In triangle RAS and triangle QAT

`\angle R =\angle Q` [Angle]

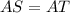`AS =AT` [Side] [Given]

By Base Angle Theorem states that in an isosceles triangle(i.e, AST), the angles opposite the congruent sides(AS =AT) are congruent.

⇒
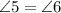`\angle 5= \angle 6` [By base ∠'s of isosceles triangle are equal]

By definition of supplementary angles, if two Angles are Supplementary when they add up to 180 degrees.

`\angle 4`,
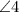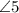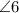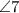`\angle 5` are supplementary 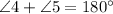and
`\angle 6`,
`\angle 7` are supplementary.

⇒
`\angle 4+ \angle 5 =180^(\circ)` and

`\angle 6+ \angle 7 =180^(\circ)`

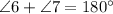
Two
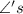`\angle 's` supplementary to equal
`\angle 's`

`\angle 4+ \angle 5 =\angle 6+ \angle 7`

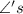
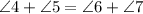
Since,
`\angle 5 =\angle 6`

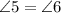
then, we get;

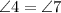`\angle 4 =\angle 7` [Angle]

then, by AAS postulates,

`\triangle RAS \cong \triangle QAT`

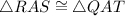
By CPCT[Corresponding Part of Congruent Triangles are equal]

`RS = QT` Hence Proved!