If the points P (7, 12), Q (-3, -12) and R (14, 5) lie on a circle with the center C (0, 2), then the distance OP, OQ and OR are the same.
The formula of a distance between two points:
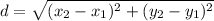
Substitute:
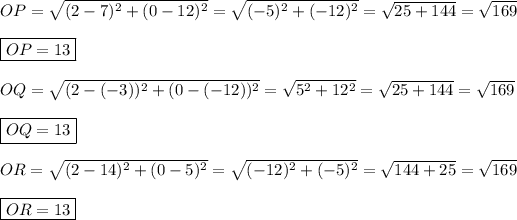
OP = OQ = OR, therefore the points P, Q and R lie on one circle.