Answer:
1.
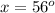
2. Exterior angle =
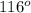
Step-by-step explanation:
1.
We can see from our given diagram that (2x+4) degrees is the measure of exterior angle of triangle PQR.
Since the measure of exterior angle of a triangle equals to the sum of the opposite interior angles. So measure of our given triangle's exterior angle will be equal to sum of measure of angle P and angle Q.
We can represent this information as:
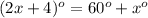
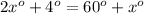
Let us subtract
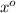 from both sides of our equation.
from both sides of our equation.
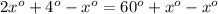
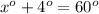
Let us subtract
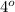 from both sides of our equation.
from both sides of our equation.
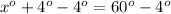
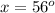
Therefore, value of x is 56 degrees.
2. Since the measure of exterior angle of our given triangle is 2x+4, let us substitute x=56 in our expression to find the measure of exterior angle.
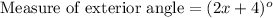
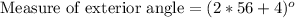
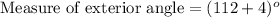
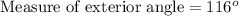
Therefore, the measure of exterior angle of our given triangle is 116 degrees.