Question

The population of deer forest is currently 800 individuals. Scientists predict that this population will grow at a rate of 20 percent per year.

Answer 1

3.5 years

Explanation:

Answer 2

C. 3.8 years

Explanation:

Exponential Growth

The natural growth of some magnitudes can be modeled by the equation:

`P(t)=P_o(1+r)^t`

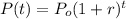
Where P is the actual amount of the magnitude, Po is its initial amount, r is the growth rate and t is the time.

The actual population of deer in a forest is Po=800 individuals. It's been predicted the population will grow at a rate of 20% per year (r=0.2).

We have enough information to write the exponential model:

`P(t)=800(1+0.2)^t`

`P(t)=800(1.2)^t`

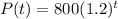
It's required to find the number of years required for the population of deers to double, that is, P = 2*Po = 1600. We need to solve for t:

`800(1.2)^t=1600`

Dividing by 800:

`(1.2)^t=1600/800=2`

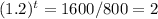
Taking logarithms:

`t\log 1.2=\log 2`

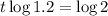
Dividing by log 1.2:

`t=(\log 2)/( \log 1.2)`

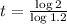
Calculating:

t = 3.8 years

Answer: C. 3.8 years