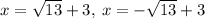Question

Find the zeros of y = x2 – 6x – 4 by completing the square.

Answer 1

The solutions to the quadratic equations are:

`x=√(13)+3,\:x=-√(13)+3`

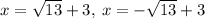
Explanation:

Given the function

`y\:=\:x^2\:-\:6x\:-\:4`

substitute y = 0 in the equation to determine the zeros

`0\:=\:x^2\:-\:6x\:-\:4`

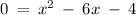
Switch sides

`x^2-6x-4=0`

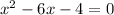
Add 4 to both sides

`x^2-6x-4+4=0+4`

Simplify

`x^2-6x=4`

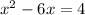
Rewrite in the form (x+a)² = b

But, in order to rewrite in the form x²+2ax+a²

Solve for 'a'

2ax = -6x

a = -3

so add a² = (-3)² to both sides

`x^2-6x+\left(-3\right)^2=4+\left(-3\right)^2`

`x^2-6x+\left(-3\right)^2=13`

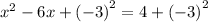
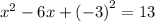
Apply perfect square formula: (a-b)² = a²-2ab+b²

`\left(x-3\right)^2=13`

`\mathrm{For\:}f^2\left(x\right)=a\mathrm{\:the\:solutions\:are\:}f\left(x\right)=√(a),\:-√(a)`

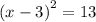
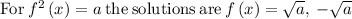
solve

`x-3=√(13)`

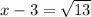
Add 3 to both sides

`x-3+3=√(13)+3`

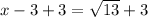
Simplify

`x=√(13)+3`

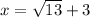
now solving

`x-3=-√(13)`

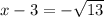
Add 3 to both sides

`x-3+3=-√(13)+3`

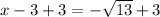
Simplify

`x=-√(13)+3`

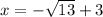
Thus, the solutions to the quadratic equations are:

`x=√(13)+3,\:x=-√(13)+3`