Question

Find the ratio of the volume of one sphere to the volume of the right cylinder

Answer 1

B

Explanation:

Let
`r` be the radius of one sphere.

• Volume of sphere is
  `V=(4)/(3)\pi r^3`

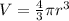
Since radius is r, the height of the cylinder will be
`4r`

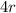
Also, the cylinder has the same radius as the sphere:
`r`

• Volume of Cylinder is
  `V=\pi r^2 h`

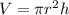
Plugging in the values we get:
`V=\pi (r)^(2)(4r)=4\pi r^3`

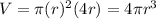
Ratio of volume of 1 sphere to volume of cylinder is:

`((4)/(3)\pi r^3)/(4\pi r^3)=((4)/(3))/(4)=(4)/(3)*(1)/(4)=(1)/(3)`

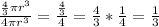
The ratio is 1:3

Answer choice B is right.