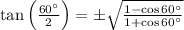Question

Given x = 60°, tan x/2 can be rewritten as which of the following?

1-cos60/1-2sin^260

+- SQRT 1-cos60/1+cos60

tan60/2tan^260

+- SQRT 1-cos60/2

Answer 1

Answer: Choice B

I'm assuming choice B shows the quantity (1-cos(60)) all over the quantity (1+cos(60)), and that is one big fraction under the square root.

The trig identity we'll use is what I'm showing in the attached images below. All we do is replace theta with 60 and that's all there is to it. An identity like that is either memorized or you will have it handy on a notecard or reference sheet.

Answer 2

`\pm \sqrt{(1-\cos 60^(\circ))/(1+\cos 60^(\circ))}`

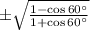
Explanation:

Tangent function is one of the trigonometric function such that
`\tan \theta =(\sin \theta )/(\cos \theta )`

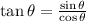
Basically, we can also say that tangent function is ratio of side opposite to the angle and side adjacent to the angle.

Given:
`x=60^(\circ)`

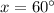
We need to rewrite
`\tan \left ( (x)/(2) \right )`.

As
`\tan \left (x \right )=\pm \sqrt{(1-\cos 2x)/(1+\cos 2x)}`

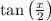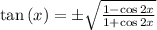
As we need to express
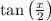`\tan \left ( (x)/(2) \right )`, divide angle by 2, we get,

`\tan \left ( (x)/(2) \right )=\pm \sqrt{(1-\cos x)/(1+\cos x)}`

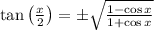
At
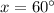`x=60^(\circ)`,

`\tan \left ( (60^(\circ))/(2) \right )=\pm \sqrt{(1-\cos 60^(\circ))/(1+\cos 60^(\circ))}`