Answer: Choice B (1,-2)
note: I'm assuming there is a "less than or equal to" sign as part of the given inequality, rather than a simple "less than" sign (without the "or equal to" part)
============================================
Work Shown:
Plug in x = -2 and y = 4 from the point (x,y) = (-2, 4). Then simplify. If you get a true statement, then this is a solution point
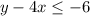
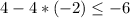
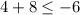

This statement is false. The value 12 is not to the left of -6 on the number line, nor is 12 equal to -6. So (x,y) = (-2,4) is not a solution
-------------
Plug in x = 1 and y = -2
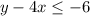
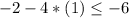

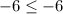
This statement is true, but only if the inequality sign is a "less than or equal to" sign. Otherwise, the statement is false because -6 cannot be smaller than itself.
-------------
Plug in x = 1 and y = 3
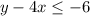

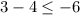
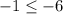
Like choice A, this is false. So (x,y) = (1,3) is not a solution
-------------
Plug in x = 2 and y = 3
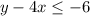
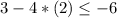
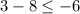
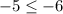
We end up with another false statement. So (x,y) = (2,3) isn't a solution either.