Question

Verify the identity. 4 csc 2x = 2 csc2x tan x

Answer 1

Explanation:

`4csc(2x) = 2csc^2(x) tan(x)`

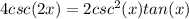
We start with Left hand side

We know that csc(x) = 1/ sin(x)

So csc(2x) is replaced by 1/sin(2x)

`4 (1)/(sin(2x))`

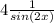
Also we use identity

sin(2x) = 2 sin(x) cos(x)

`4 (1)/(2sin(x)cos(x))`

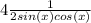
4 divide by 2 is 2

Now we multiply top and bottom by sin(x) because we need tan(x) in our answer

`2(1*sin(x))/(sin(x)cos(x)*sin(x))`

`2(sin(x))/(sin^2(x)cos(x))`

`2(1)/(sin^2(x)) (sin(x))/(cos(x))`

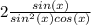
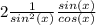
We know that sinx/ cosx = tan(x)

Also 1/ sin(x)= csc(x)

so it becomes 2csc^2(x) tan(x) , Right hand side

Hence verified