Question

What is the modulus of |9+40i|?

Answer 1

Answer: Modulus of |9+40i| =41

Explanation:

Since we have given that

`z=\mid9+40i\mid`

Here,

`z=a+bi\\\\where,\\\\a=\text{real number}=9\\\\b=\text{imaginary number}=40`

We need to find the modulus of z:

`\mid z\mid=√(a^2+b^2)`

`\mid z\mid=√(9^2+40^2)\\\\\mid z\mid=√(81+1600)\\\\\mid z\mid=√(1681)\\\\\mid z\mid=41`

Hence, Modulus of |9+40i| =41

Answer 2

41

Explanation:

We know that complex numbers are a combination of real and imaginary numbers

Real part is x and imaginary part y is multiplied by i, square root of -1

Modulus of x+iy =
`√(x^2+y^2)`

Here instead of x and y are given 9 and 40

i.e. 9+40i

Hence to find modulus we square the coefficients add them and then find square root

|9+49i| =
`√(9^2+40^2) =√(1681)`

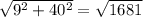
By long division method we find that

|9+40i| =41