Question

Which graph represents the function? f(x)=(x+2)^2 if x<−1

|x|+1     if −1≤x≤1

−√x        if x>1

Answer 1

option B

Explanation:

I took the test

Answer 2

option B

Explanation:

To get the graph of piecewise function

We make a table for each function

Plug in end points and make a table

First function f(x) = (x+2)^2 if x<-1

x <-1 so we pick number for x less than -1. Also we use -1 but we use open circle at x=-1

x y = (x+2)^2

-3 (-3+2)^2= 1

-2 (-2+2)^2 = 0

-1 (-1+2)^2 = 1

Now plot the table on graph

second function f(x) = |x| + 1 if -1<=x<=1

Make a table, we use -1, 0 and 1 because we have -1<=x<=1 (-1 and 1 are included)

x y=|x| +1

-1 |1| + 1 = 2

0 |0|+1 = 1

1 |1|+1= 2

Third function
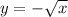`y=-√(x)` if x>1

We find out y when x=1 and make a open circle at x=1 because we have x>1

x
`y=-√(x)`

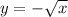
1
`-√(1)=-1`

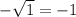
4
`-√(4)=-2`

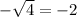
Plot all the point on the graph

Correct graph is attached below