Question

Seven-eighths of a sample of hydrogen-3 will have become a stable isotope after 36.9 years. What is the half-life of hydrogen-3? 12.3 years 18.5 years 32.3 years 36.9 years

Answer 1

A. 12.3 years

Step-by-step explanation:

Answer 2

12.3 years

Step-by-step explanation:

The equation of the radioactive decay can be written as follows:

`(N(t))/(N_0)=((1)/(2))^{(t)/(\tau_(1/2))}` (1)

where

N(t) is the amount of radioactive sample left at time t

N0 is the amount of radioactive sample at time t=0

t is the time passed

`\tau_(1/2)` is the half-life of the isotope

The problem tells us that after t=36.9 y, the amount of sample which has become stable is 7/8. This means that 7/8 of the sample has already decayed, so the amount of radioactive sample left is

`(N(t))/(N_0)=1-(7)/(8)=(1)/(8)`

We can now re-arrange equation (1) by using this information and by substituting t=36.9 y we find:

`(t)/(\tau_(1/2))=log_(1/2) ((N(t)))/(N_0))\\\tau_(1/2)=(t)/(log_(1/2)((N(t))/(N_0)))=(36.9 y)/(log_(1/2)(1/8))=(36.9 y)/(3)=12.3 y`

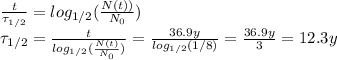
So, the answer is

12.3 years