Question

The length of a rectangle is the sum of the width and one. The area direct angle 72 units. What’s the length, in units, of the rectangle

Answer 1

The length of the rectangle is of 9 units.

Explanation:

Solving a quadratic equation:

Given a second order polynomial expressed by the following equation:

`ax^(2) + bx + c, a\\eq0`.

This polynomial has roots
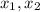`x_(1), x_(2)` such that
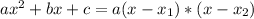`ax^(2) + bx + c = a(x - x_(1))*(x - x_(2))`, given by the following formulas:

`x_(1) = (-b + √(\bigtriangleup))/(2*a)`

`x_(2) = (-b - √(\bigtriangleup))/(2*a)`

`\bigtriangleup = b^(2) - 4ac`

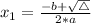
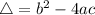
Area of a rectangle:

A rectangle has width
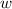`w` and length
`l`. The area is the multiplication of these measures, that is:

`A = wl`

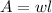
The length of a rectangle is the sum of the width and one.

This means that
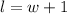`l = w+1`, or
`w = l - 1`

The area direct angle 72 units. What’s the length, in units, of the rectangle

We want to find the length. So

`wl = 72`

`(l-1)l = 72`

`l^2 - l - 72 = 0`

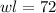
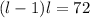
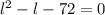
Quadratic equation with
`a = 1, b = -1, c = -72`. So

`\bigtriangleup = (-1)^(2) - 4(1)(-72) = 289`

`l_(1) = (-(-1) + √(289))/(2*(1)) = 9`

`l_(2) = (-(-1) - √(289))/(2*(1)) = -8`

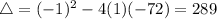
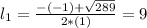
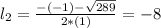
Since the length is a positive measure, the length of the rectangle is of 9 units.