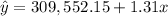Answer:
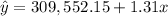
Explanation:
The equation for the least-squares regression is,
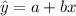
where b is the slope and a is the intercept.
They can be found out by,
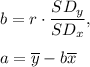
where,
r = correlation coefficient = 0.84
 = standard deviation of y = 44,910
= standard deviation of y = 44,910
 = standard deviation of x = 28,803
= standard deviation of x = 28,803
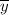 = mean of y = 774,140
= mean of y = 774,140
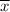 = mean of x = 354,718
= mean of x = 354,718
Putting the values,


Therefore the equation is,