Question

All the select drop box is. are not and are

Answer 1

Explanation:

Corresponding angles of both the squares are congruent. (angles of a square measure 90°)

Ratio of the sides of the given squares =
`\frac{\text{Side length of small square}}{\text{Side length of the large square}}`

=
`(2)/(5)`

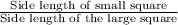
This ratio of side lengths is constant for all corresponding sides.

Therefore, corresponding sides are proportional.

Since, all angles of both the squares are congruent and all the sides are proportional, both the squares will be similar.

Scale factor =
`\frac{\text{Side length of large square}}{\text{Side length of the smaller square}}`

=
`(5)/(2)`

= 2.5

This sequence of similarity transformations shows the figures are similar.