Question

I really need help. This is very confusing for me. NEED HELP!!!

Answer 1

(16)

Given the statement: Elmwood st. and oak Dr. are the same distance.

All intersection are perpendicular.

To prove that: Peach Dr. tree is the same distance as Sycamore Ln.

It given that all the intersection are perpendicular which means each interior angles are of
`90^(\circ)`

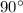
By rectangle properties:

• Each of the interior angles are
  `90^(\circ)`
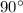
• The opposite sides of the rectangle are equal
• The diagonal of a rectangles bisects each other.

Since, Elmwood st. and oak Dr. are the same distance.

then, by rectangle properties;

Peach Dr. tree is the same distance as Sycamore Ln proved!

6.10

(11)

Given:
`\angle A \cong \angle T` ,
`\overline{MA} \cong \overline{HT}`

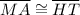
To prove:
`\triangle MAX \cong \triangle HTX`

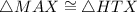
In ΔMAX and ΔHTX

`\angle A \cong \angle T` [Angle] [Given]

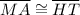`\overline{MA} \cong \overline{HT}` [Side] [Given]

Vertical angle theorem states that angles that are opposite each other.

Since, these angles are formed when two lines cross each other.

And also vertical angles are congruent to each other.

Since,
`\angle MXA` ,
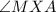`\angle HXT` are vertical angles

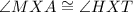`\angle MXA \cong \angle HXT` [Vertical angles are congruent]

AAS (Angle-Angle-Side) theorem states that if two angles and a non-included side in one triangle are congruent to two corresponding angles and a non-included side in another triangle, then those triangles are congruent.

Then, by AAS theorem,

`\triangle MAX \cong \triangle HTX`

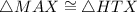
(14)

Given:
`\overline{AX} \cong \overline{TX}` ,
`\angle A \cong \angle T`

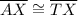Prove that:
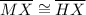
`\overline{MX} \cong \overline{HX}`

In
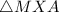`\triangle MXA` and
`\triangle HXT`

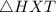
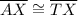`\overline{AX} \cong \overline{TX}` [Side] [Given]

`\angle A \cong \angle T` [Angle] [Given]

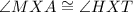`\angle MXA \cong \angle HXT` [Vertical angles are congruent]

ASA (Angle -Side-Angle) theorem states that if two angles and the included side of one triangle are congruent to the corresponding parts of another triangle, then these triangles are congruent.

then by ASA theorem;

`\triangle MAX \cong \triangle HTX`

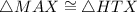
CPCT [Corresponding Part of Congruent triangles are congruent.]

⇒
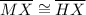`\overline{MX} \cong \overline{HX}` [By CPCT] proved!