Question

Write the first five terms of the the sequence defined by the explicit formula an=72(1/3)^n-1

Answer 1

The first five terms are as follows:

72, 24, 8, 2.66, 0.88

Explanation:

1) Explicit formula:

`72 * 1/3^(n-1)`

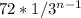
2) Simply replace "n" with 2,3,4 and 5 in order to find the numbers associated with these terms.

a(1) = 72

a(2) = 24

a(3) = 8

a(4) = 2.66

a(5) = 0.88

Note:

In the explicit formula the first term is already provided, so you do not have to find the first term if it has already been given.

Answer 2

`a_n=72\left((1)/(3)\right)^(n-1)\\\\\text{Put}\ n=1,\ n=2,\ n=3,\ n=4,\ n=5\ \text{to the equation}:\\\\n=1\to a_1=72\left((1)/(3)\right)^(1-1)=72\left((1)/(3)\right)^0=72(1)=72\\\\n=2\to a_2=72\left((1)/(3)\right)^(2-1)=72\left((1)/(3)\right)^1=72\left((1)/(3)\right)=(72)/(3)=24\\\\n=3\to a_3=72\left((1)/(3)\right)^(3-1)=72\left((1)/(3)\right)^2=72\left((1)/(9)\right)=(72)/(9)=8\\\\n=4\to a_4=72\left((1)/(3)\right)^(4-1)=72\left((1)/(3)\right)^3=72\left((1)/(27)\right)=(72)/(27)=(8)/(3)\\\\n=5\to a_5=72\left((1)/(3)\right)^(5-1)=72\left((1)/(3)\right)^4=72\left((1)/(81)\right)=(72)/(81)=(8)/(9)\\\\Answer:\ \boxed{72,\ 24,\ 8,\ (8)/(3),\ (8)/(9)}`