Question

SOS I literally have NO idea how to do 9-11!!! If anyone knows how plz help. Thank u so much❤️❤️❤️

Answer 1

Steps:

So before we jump into these problems, we must keep this particular rule in mind:

• Product Rule of Radicals: √ab = √a × √b. Additionally, remember that √a × √a = a

9.

So remember that the perimeter is the sum of all the sides. In this case:

`P=3√(12) +√(27) +2√(48)`

So firstly, using the product rule of radicals we need to simplify these radicals as such:

`3√(12) =3*√(4)*√(3) =3*2*√(3)=6√(3)\\√(27) =√(9) *√(3) =3√(3) \\2√(48)=2*√(8)*√(6)=2*√(4)*√(2)*√(2)*√(3)=2*2*2*√(3)=8√(3)\\\\P=6√(3)+3√(3)+8√(3)`

Now, combine like terms (since they all have the same like term √3, they can all be added up):

`P=6√(3)+3√(3)+8√(3)\\P=17√(3)`

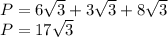
Your final answer is 17√3 in.

10a.

For this, we will be using the pythagorean theorem, which is
`a^2+b^2=c^2` , where a and b are the legs of the right triangle and c is the hypotenuse of the triangle. In this case, √18 and √32 are our legs and we need to find the hypotenuse. Set up our equation as such:

`(√(18) )^2+(√(32))^2=c^2`

From here we can solve for the hypotenuse. Firstly, solve the exponents (remember that square roots and squared power cancel each other out):

`18+32=c^2`

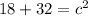
Next, add up the left side:

`50=c^2`

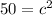
Lastly, square root both sides of the equation:

`√(50)=c`

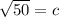
The hypotenuse is √50 cm.

10b.

Now, the process is similar to that of 9 so I will just show the steps to the final answer.

`P=√(18) +√(32) +√(50) \\\\√(18)=√(9)*√(2)=3√(2)\\√(32)=√(16)*√(2)=4√(2)\\√(50)=√(25)*√(2)=5√(2)\\\\P=3√(2)+4√(2)+5√(2)\\P=12√(2)`

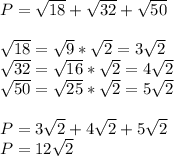
The perimeter is 12√2 in.

11.

Now, the process is still similar to question 9 but remember that this time we are working with cube roots.

`P=3\sqrt[3]{24} +\sqrt[3]{27}+2\sqrt[3]{81}\\\\3\sqrt[3]{24}=3*\sqrt[3]{8}*\sqrt[3]{3}=3*2*\sqrt[3]{3}=6\sqrt[3]{3}\\\sqrt[3]{27}=3\\2\sqrt[3]{81}=2*\sqrt[3]{27}*\sqrt[3]{3}=2*3*\sqrt[3]{3}=6\sqrt[3]{3}\\\\P=6\sqrt[3]{3}+3+6\sqrt[3]{3}\\P=3+12\sqrt[3]{3}`

Note that when adding the numbers together, 3 isn't a like term to the other 2 terms because it doesn't have ∛3 multiplied with it.

The perimeter is 3 + 12∛3 in.