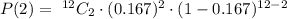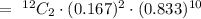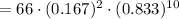Answer:
The probability that exactly 2 of the rolls is a sum of 7 will is 0.296
Explanation:
The probability of rolling a sum of 7 when rolling two dice simultaneously is 0.167.
Let us assume that, A be the event that the sum is 7. So,
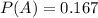
Binomial probability represents the probability that a binomial experiment results (i.e either success or failure or only two results) in exactly x successes.
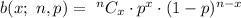
So the probability that exactly 2 of the rolls is a sum of 7 will be,