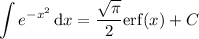Question

Solve the integral:

`\int \: {e}^{ - {x}^(2) } dx`

Answer 1

`e^(-x^2)` has no antiderivative in terms of elementary functions (polynomials, exponentials, logarithms, trigonometric functions, etc), but there is a special function defined to fit that role called the error function,
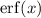`\mathrm{erf}(x)`, where

`\mathrm{erf}(x)=\displaystyle\frac2{\sqrt\pi}\int_0^xe^(-t^2)\,\mathrm dt`

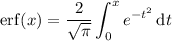
By the fundamental theorem of calculus, we can see that

`(\mathrm d)/(\mathrm dx)\mathrm{erf}(x)=\frac2{\sqrt\pi}e^(-x^2)`

which means we have

`\displaystyle\int e^(-x^2)\,\mathrm dx=\frac{\sqrt\pi}2\mathrm{erf}(x)+C`