Question

PLEASE HELP ASAP!!! CORRECT ANSWERS ONLY PLEASE!!

A population of bacteria is growing according to the exponential model P = 100e^(.70)t, where P is the number of colonies and t is measured in hours. After how many hours will 300 colonies be present? [Round answer to the nearest tenth.]

Answer 1

Option B. 1.6 Hours

Explanation:

The model for the population of bacteria is growing by :

`P=100e^((0.70)t)`

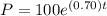
Where P = Number of colonies

and t = time in hours.

So, now put the value of P = 300 in the given model and obtain the value of t.

⇒
`300=100e^((0.70)t)`

⇒
`3=e^((0.7)t)`

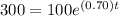
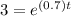
Taking the natural log in on both the side

⇒
`In3=Ine^((0.7)t)`

⇒
`In3=0.7t`

⇒
`t=(In3)/(0.7)`

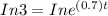
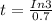
⇒ t = 1.6 hours

Therefore, The correct option is B). 1.6 hours

Answer 2

Answer: B

Explanation:

`P=100e^((.70)t)`

`300=100e^(.7t)`

`3=e^(.7t)`

`ln3=lne^(.7t)`

`ln3=.7t`

`(ln3)/(.7)=t`

1.6 = t