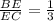Answer:
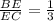
Explanation:
In the diagram below we have
ABCD is a parallelogram. K is the point on diagonal BD, such that
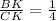
And AK meets BC at E
now in Δ AKD and Δ BKE
∠AKD =∠BKE ( vertically opposite angles are equal)
since BC ║ AD and BD is transversal
∠ADK = ∠KBE ( alternate interior angles are equal )
By angle angle (AA) similarity theorem
Δ ADK and Δ EBK are similar
so we have
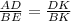

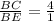 ( ABCD is parallelogram so AD=BC)
( ABCD is parallelogram so AD=BC)
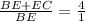 ( BC= BE+EC)
( BC= BE+EC)
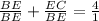
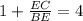
 ( subtracting 1 from both side )
( subtracting 1 from both side )
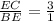
taking reciprocal both side