Answer:
a. α and β
Explanation:
One way to solve this exercise is by analyzing the y - intercept of the functions.
By looking at the graph, we can see that II and IV have the same y - intercept.
All the formulas below depend of the variable ''
 '' so if we want to find the y - intercept we only need to replace by ''
'' so if we want to find the y - intercept we only need to replace by ''
 '' in the formulas.
'' in the formulas.
We can also see that the y - intercept of II and IV will be the lower that the another y - intercept of the functions.
If we replace by
 :
:
(α)(t) =
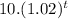 ⇒
⇒
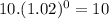
(β)(t) =
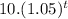 ⇒
⇒
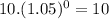
(χ)(t) =
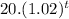 ⇒
⇒
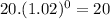
(δ)(t) =
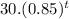 ⇒
⇒
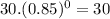
(ε)(t) =
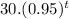 ⇒
⇒
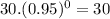
(Φ)(t) =
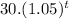 ⇒
⇒
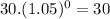
We find that the lowest y - intercept (also equal) are the y - intercept of α and β. Therefore, the correct option is a. α and β