Question

PLEASE HELP 30 POINTS!!!!!!!!!!!!!!!!!!!!!!!

The table below shows some values of f(x) and g(x) for different values of x:

Complete the chart and determine the solution of the equation f(x) = g(x).
x = −1
x = 0
x = 2
x = 25

Answer 1

Since you know the value of "x", you can plug in the value for "x" in the equation.

[When an exponent is negative, you move it to the other side of the fraction to make the exponent positive.]

For example:

`x^(-2)` or
`(x^(-2))/(1) =(1)/(x^2)`

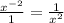
`(1)/(y^(-3)) =(y^3)/(1)` or y³

x = -2

f(x) = 9x + 7

f(-2) = 9(-2) + 7 = -18 + 7 = -11

`g(x)=5^x`

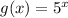
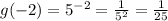`g(-2)=5^(-2)=(1)/(5^2)=(1)/(25)` (idk if you should have it as a decimal or a fraction)

x = -1

f(x) = 9x + 7

f(-1) = 9(-1) + 7 = -9 + 7 = -2

`g(x)=5^x`

`g(-1)=5^(-1)=(1)/(5)`

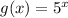
x = 0

f(x) = 9x + 7

f(0) = 9(0) + 7 = 7

`g(x)=5^x`

`g(0)=5^0=1`

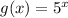
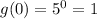
x = 1

f(x) = 9x + 7

f(1) = 9(1) + 7 = 9 + 7 = 16

`g(x)=5^x`

`g(1)=5^1=5`

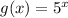
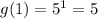
x = 2

f(x) = 9x + 7

f(2) = 9(2) + 7 = 18 + 7 = 25

`g(x)=5^x`

`g(2)=5^2=25`

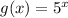
You need to determine the solution of f(x) = g(x)

Since you know f(x) = 9x + 7 and
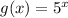`g(x)=5^x`, you can plug in (9x + 7) for f(x), and (
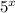`5^x`) into g(x)

f(x) = g(x)

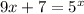`9x+7=5^x` You can plug in each value of x into the equation

Your answer is x = 2 because when you plug in 2 for x in the equation, you get 25 = 25