Question

Log(base)4(3x-7)=log(base)4(x-15)

Could somebody help me out with this question? I don't even know where to begin.

Answer 1

The bases of the logarithms on either side of the equation are the same, which means that their arguments must be the same:

`\log_4(3x-7)=\log_4(x-15)\implies3x-7=x-15`

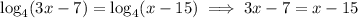
Put another way, we can write both sides as powers of 4, then simplify and eliminate the logarithms:

`\log_4(3x-7)=\log_4(x-15)\implies4^(\log_4(3x-7))=4^(\log_4(x-15))\implies3x-7=x-15`

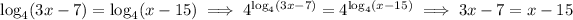
Then solve for
`x`:

`3x-7=x-15\implies2x=-8\implies x=-4`

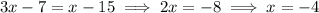
Then we just have to check if this solution is valid. On the left side, we have

`\log_4(3(-4)-7)=\log_4(-15)`

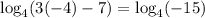
but we can't take logarithms of negative numbers, so there is no solution, as long as we're using the real-valued logarithm, anyway;
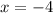`x=-4` is a solution if we use the complex-valued version.