Question

I would appreciate it if you could answer the questions please- A ball is thrown upward at 48ft/s from a building that is 100 feet high the function h(t)= -16+84t + 100 expresses the balls height,h in feet given the time t, in seconds since the ball was thrown.please answer the questions if you know the answer I would appreciate it

Answer 1

(I'm not sure if your teacher is nit-picky about significant figures, but here I go...)

8) 1.5 seconds

9) 136 feet

10) 4.415 seconds

11) 2.5 seconds (also 0.5 seconds)

Explanation:

See attached screenshot of Desmos graph showing y(t) = -16t² + 48t + 100, y = 120 and respective points.

Answer 2

Problem 8

Answer: 1.5 seconds

----------------

Work Shown:

h(t) = -16t^2+48t+100 is the same as y = -16x^2+48x+100, just with different variables.

Compare this to y = ax^2+bx+c to find that a = -16, b = 48, c = 100

Then compute the x coordinate of the vertex -b/(2a) getting

h = -b/(2a)

h = -48/(2*(-16))

h = 1.5

It takes 1.5 seconds for the ball to reach its peak height. The vertex represents the max height since the parabola opens downward.

==============================================

Problem 9

Answer: 136 feet

----------------

Work Shown:

Plug the result from problem 8 into the function

y = -16x^2 + 48x + 100

y = -16(1.5)^2 + 48(1.5) + 100

y = 136

The vertex is (1.5, 136)

This means at 1.5 seconds, the ball is 136 feet off the ground at its highest point.

==============================================

Problem 10

Answer: approximately 4.415 seconds

----------------

Work Shown:

Plug in y = 0 and solve for x

y = -16x^2 + 48x + 100

0 = -16x^2 + 48x + 100

-16x^2 + 48x + 100 = 0

Apply the quadratic formula

`x = (-b\pm√(b^2-4ac))/(2a)\\\\x = (-(48)\pm√((48)^2-4(-16)(100)))/(2(-16))\\\\x = (-48\pm√(8704))/(-32)\\\\x \approx (-48\pm93.29523032)/(-32)\\\\x \approx (-48+93.29523032)/(-32)\ \text{ or } \ x \approx (-48-93.29523032)/(-32)\\\\x \approx (45.29523032)/(-32)\ \text{ or } \ x \approx (-141.2952303)/(-32)\\\\x \approx -1.41547593\ \text{ or } \ x \approx 4.41547595\\\\`

A negative x value makes no sense because time cannot be negative, so we ignore the first solution. The only practical solution is roughly x = 4.415

It takes approximately 4.415 seconds for the ball to reach the ground.

==============================================

Problem 11

2 Answers: At 0.5 seconds and at 2.5 seconds

----------------

Work Shown:

Use the same idea as problem 10. Instead of y = 0, use y = 120

y = -16x^2 + 48x + 100

120 = -16x^2 + 48x + 100

-16x^2 + 48x + 100 = 120

-16x^2 + 48x + 100-120 = 0

-16x^2 + 48x - 20 = 0

-4(4x^2 - 12x + 5) = 0

4x^2 - 12x + 5 = 0

Now apply the quadratic formula

`x = (-b\pm√(b^2-4ac))/(2a)\\\\x = (-(-12)\pm√((-12)^2-4(4)(5)))/(2(4))\\\\x = (12\pm√(64))/(8)\\\\x = (12\pm8)/(8)\\\\x = (12+8)/(8)\ \text{ or } \ x = (12-8)/(8)\\\\x = (20)/(8)\ \text{ or } \ x = (4)/(8)\\\\x = 2.5\ \text{ or } \ x = 0.5\\\\`

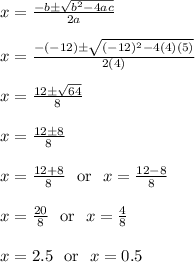
There are two moments in time when the ball is 120 feet in the air. Those two moments are at x = 0.5 seconds and at x = 2.5 seconds.

At x = 0.5, the ball is going upward. At x = 2.5, the ball is coming back down.