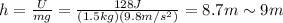Answer:
9 m
Step-by-step explanation:
The elastic potential energy initially stored in the spring is given by:
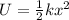
where
k = 2500 N/m is the spring constant
x = 32 cm = 0.32 m is the compression of the spring
Substituting:
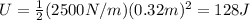
Due to the law of conservation of energy, when the spring is released all this energy is converted into kinetic energy of the rock, which starts moving upward. As the rock reaches its maximum height, all the energy has been converted into gravitational potential energy:
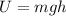
where
m = 1.5 kg is the rock's mass
g = 9.8 m/s^2 is the gravitational acceleration
h = ? is the maximum height reached by the rock
Using U=128 J, we find h: