Question

I Consumer Economics Suppose your car contains just one gallon of gas. Driv-

ing at 20 mi/h you can go 26 mi. Likewise, you can go 34 mi driving at
40 mi/h and 32 mi driving at 50 mi/h.
a. Find a quadratic function that models this data.
b. How far could you go if you drove at 65 mi/h?
c. The nearest gas station is 16 mi away. If the speed limit is 55 mi/h, at what
maximum speed could you drive and still reach it?

Answer 1

See below

Explanation:

A) The quadratic function that models this data is
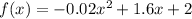`f(x)=-0.02x^2+1.6x+2` which you can view in the graph attached (done by regression).

B)
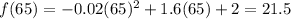`f(65)=-0.02(65)^2+1.6(65)+2=21.5`, or 21.5 miles

C) Set
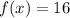`f(x)=16` and solve for x:

`f(x)=-0.02x^2+1.6x+2`

`16=-0.02x^2+1.6x+2`

`0=-0.02x^2+1.6x-14`

`x=(-b\pm√(b^2-4ac))/(2a)`

`x=(-1.6\pm√((1.6)^2-4(-0.02)(-14)))/(2(-0.02))`

`x=(-1.6\pm√(2.56-1.12))/(-0.04)`

`x=(-1.6\pm√(1.44))/(-0.04)`

`x=(-1.6\pm1.2)/(-0.04)`

`x_1=(-1.6+1.2)/(-0.04)`

`x_1=(-0.4)/(-0.04)`

`x_1=10<55`

`x_2=(-1.6-1.2)/(-0.04)`

`x_2=(-2.8)/(-0.04)`

`x_2=70>55`

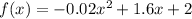
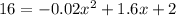
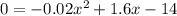
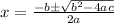
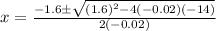
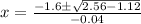
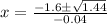
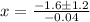
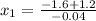
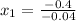
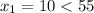
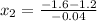
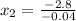
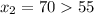
Since
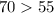`70>55`, then 10mph is the maximum speed you could drive and still reach the gas station that is 16 miles away when the speed limit is 55.