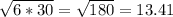Question

HW #35: similar polygons

Answer 1

Q 9:

Because the two polygons are similar so AB ≈ PQ = SR

Scale factor is 25/20 = 1.25

Perimeter of ABCD = 14+20+14+20 = 68

We can find the length of SP by multiplying the scale factor with the AD so

SP = 14 * 1.24= 17.5

Perimeter of PQRS = 17.5+25+17.5+25 = 85

-----------------------------------------------------------------------------------

Q 10:

Because the two polygons are similar so AD ≈. EH

Scale factor is 7/14 = 0.5

Perimeter of ABCD = 12+14+13+26 = 65

Because the two polygons are similar so DC ≈ HG

and our scale factor is 0.5 so HG = 13/2 = 6.5

Perimeter of EFHG = 6 + 7 + 6.5 + 13 = 32.5

----------------------------------------------------------------------------------

Q 11:

The Geometric Mean is a special type of average where we multiply the numbers together and then take a square root (for two numbers). And the formula for finding the Geometric mean of two numbers a and b is

`√(a*b)`

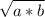
So geometric mean of the 8 and 10 can be found as

`√(8*2) = √(16) = 4`

-----------------------------------------------------------------------------------

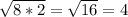
Q 12:

Similarly we can using the above formula of finding the geometric mean of 5 and 45 as

`√(5*45) = √(225) = 15`

-------------------------------------------------------------------------------

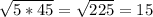
Q 13:

and we can find the geometric mean of 6 and 30 by using the same formula

`√(6*30) = √(180) = 13.41`