Question

∆ABC is transformed with the center of dilation at the origin.

Pre-image: ∆ABC with vertices A(2, 5), B(6, 10), C(9, −1)
Image: ∆A'B'C' with vertices A' (0.5, 1.25), B' (1.5, 2.5), C' (2.25, −0.25)
What is the scale factor of the dilation that maps the pre-image to the image?

Answer 1

1/4

Explanation:

We are to find the scale factor of the dilation that maps the pre-image of triangle ABC with vertices A(2, 5), B(6, 10) and C(9, −1) to the image triangle A'B'C' with vertices A' (0.5, 1.25), B' (1.5, 2.5), C' (2.25, −0.25).

Center of dilation is at the origin.

To find the scale factor, we will divide the corresponding vertices of the image and pre-image.

A(2, 5) ---> A' (0.5, 1.25) =
`(0.5)/(2) , (1.25)/(5)=((1)/(4) , (1)/(4))`

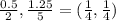
B(6, 10) ---> B' (1.5, 2.5) =
`(1.5)/(6) , (2.5)/(10)=((1)/(4) , (1)/(4))`

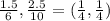
C(9, −1) ---> C' (2.25, −0.25) =
`(2.25)/(9) , (-0.25)/(-1)=((1)/(4) , (1)/(4))`

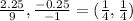
Therefore, the scale factor of the dilation is 1/4.