Question

∆ABC is transformed with the center of dilation at the origin.

Pre-image: ∆ABC with vertices A(−5, −4), B(−7, 3), C(3, −2)
Image: ∆A'B'C' with vertices A' (−3.75, −3), B' (−5.25, 2.25), C' (2.25, −1.5)
What is the scale factor of the dilation that maps the pre-image to the image?

Answer 1

3/4

Explanation:

We are to find the scale factor of the dilation that maps the pre-image of triangle ABC with vertices A(−5, −4), B(−7, 3) and C(3, −2) to the image triangle A'B'C' with vertices A' (−3.75, −3), B' (−5.25, 2.25) and C' (2.25, −1.5).

Center of dilation is at the origin.

To find the scale factor, we will divide the corresponding vertices of the image and pre-image.

A(−5, −4) ---> A' (−3.75, −3) =
`(-3.75)/(-5) , (-3)/(-4)=((3)/(4) , (3)/(4))`

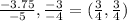
B(−7, 3) ---> B' (−5.25, 2.25) =
`(-5.25)/(-7) , (2.25)/(3)=((3)/(4) , (3)/(4))`

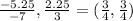
C(3, −2) ---> C' (2.25, −1.5) =
`(2.25)/(3) , (-1.5)/(-2)=((3)/(4) , (3)/(4))`

Therefore, the scale factor of the dilation is 3/4.