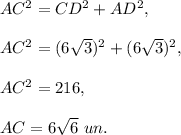Question

In ΔABC, m∠ACB = 90°, CD ⊥ AB and m∠ACD = 45°. Find AC, if CD = 6 sqrt 3

Answer 1

`AC =6√(6)`

Explanation:

In ΔACD,

AC is the hypotenuse.

CD is the adjacent side to the angle 45°.

So,
`cos 45=(CD)/(AC)`

`(1)/(√(2) ) =(6√(3) )/(AC)`

`AC=6√(3) √(2)`

`=6√(6)`

Answer 2

`6√(6)\ un.`

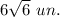
Explanation:

Consider right triangle ABC with right angle ACB. If m∠ACD = 45°, then

m∠BCD=m∠ACB-m∠ACD=90°-45°=45°.

Since CD ⊥ AB, then

m∠CDA=m∠CDB=90°.

Thus, triangles ACD and BCD are right triangles with right angles ADC and BDC. In these triangles:

m∠CAD=90°-m∠ACD=90°-45°=45°;

m∠CBD=90°-m∠BCD=90°-45°=45°.

Thus, triangles ACD and BCD are isosceles right triangles with

`CD=AD=BD=6√(3)\ un.`

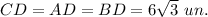
By the Pythagorean theorem,

`AC^2=CD^2+AD^2,\\ \\AC^2=(6√(3))^2+(6√(3))^2,\\ \\AC^2=216,\\ \\AC=6√(6)\ un.`