What is the shape of the graph of the function? g(x)= 3/2 (2/3) ^x

Question

asked Feb 17, 2022 136k views

1 Answer

Rasika Weragoda · Answer 1 · 2022-02-21T04:55:31+0000

Answer:

Please check the attached graph.

From the graph, it is clear that option B is the correct option.

Explanation:

Given the function

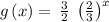
$g\left(x\right)=\:(3)/(2)\:\left((2)/(3)\right)^x$

Determining the y-intercept

We know that the value of the y-intercept can be determined by setting x = 0, and determining the corresponding value of y.

so

substituting x = 0 in the fuction

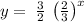
$y=\:(3)/(2)\:\left((2)/(3)\right)^x$

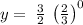
$y=\:(3)/(2)\:\left((2)/(3)\right)^0$

Apply rule:
$a^0=1,\:a\\e \:0$

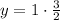
$y=1\cdot (3)/(2)$

y=(3)/(2)

y = 1.5

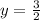
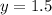
Therefore, the point representing the y-intercept is:

Determining the x-intercept

We know that the value of the x-intercept can be determined by setting y = 0, and determining the corresponding value of x.

so

substituting y = 0 in the function

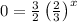
$0=(3)/(2)\left((2)/(3)\right)^x$

Using the zero factor principle

if ab=0, then a=0 or b=0 (or both a=0 and b=0)

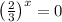
$\left((2)/(3)\right)^x=0$

We know that
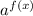$a^(f\left(x\right))$ can not be zero or negative for x ∈ R

Thus, NONE represents the x-intercept.

Please check the attached graph.

From the graph, it is clear that option B is the correct option.