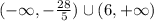QUESTION 1
The given inequality is
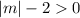
We group like terms to get,
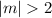
This implies that,
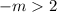 or
or
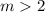 .
.
We simplify the inequality to get,
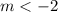 or
or
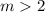 .
.
We can write this interval notation to get,
 .
.
QUESTION 2
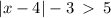 .
.
We group like terms to get,
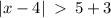 .
.
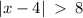
We split the absolute value sign to get,
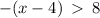 or
or

This implies that,
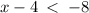 or
or

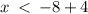 or
or
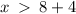
 or
or

We can write this interval notation to get,
 .
.
QUESTION 3
The given inequality is
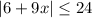
We split the absolute value sign to obtain,
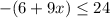 or
or
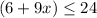
This simplifies to
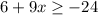 and
and

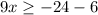 and
and
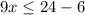
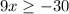 and
and
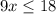
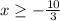 and
and

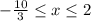
We write this in interval form to get,
![[-(10)/(3),2]](https://img.qammunity.org/2019/formulas/mathematics/high-school/oayuku7a2clwjggykcm3qitnzqgnht5rkq.png)
QUESTION 4
The given inequality is
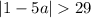
We split the absolute value sign to get,
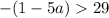 or
or
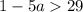
This simplifies to,
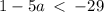 or
or
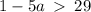
This implies that,
 or
or
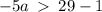
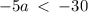 or
or

 or
or
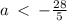
We write this in interval notation to get,