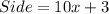Question

The area of a square rug can be represented by the expression 100x^2+60x+9. Write an expression to represent the length of each side of the rug.

Answer 1

ANSWER:

square root of ( 100x^2 + 60x + 9 )

An expression to represent the length of each side of the rug is:
square root of ( 100x^2 + 60x + 9 )

Explanation:

Let's establish that the area of a square is the length of one of its sides squared.

Area of square = Side^2

THEREFORE:

To find the length of each side of the square, we will make side the subject in the formula as displayed below.

Area of square = Side^2

Side^2 = Area of square

Side = square root of ( area of square )

From this, we will substitute the given expression for the area of the square rug to obtain the expression for the length of each side of the rug.

Side = square root of ( 100x^2 + 60x + 9 )

Answer 2

Answer : The expression to represent the length of each side of the rug is,
`Side=10x+3`

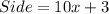
Step-by-step explanation :

As we know that the formula of area of square is:

Area of square = (Side)²

Given:

Area of square =
`100x^2+60x+9`

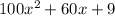
As,

Area of square = (Side)²

So,

`100x^2+60x+9=(Side)^2`

`√(100x^2+60x+9)=Side`

`√(100x^2+30x+30x+9)=Side`

`√(10x(10x+3)+3(10x+3))=Side`

`√((10x+3)(10x+3))=Side`

`√((10x+3)^2)=Side`

`(10x+3)=Side`

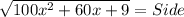
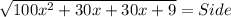
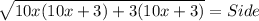
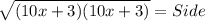
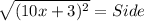
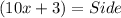
or,

`Side=10x+3`

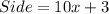
Thus, the expression to represent the length of each side of the rug is,
`Side=10x+3`