Question

Ms. Smith spent 7 hours driving from her home to Albany, a distance of 238 mi. Before noon, she averaged 32 mph. After noon she averaged 39 mph. Find the number of hours she traveled at each rate of speed.

Answer 1

ANSWER

She averaged at 32 mph for 5 hours and 39 mph for 2 hours.


Step-by-step explanation

Let

`x`
be the number of hours she travelled before noon and

`y`
be the number of hours she travelled after noon.


Then since she travelled for a total of 7 hours, we can write the equation,


`x + y = 7.....eqn(1)`



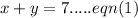
We were also given that, before noon,she averaged at 32 mph.


We know that,



`speed = (distance)/(time \: taken)`

Let

`d_1`
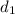
be the distance before noon.



`\Rightarrow \: 32 = (d_1)/(x)`
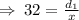
This implies that,


`d_1 = 32x`


Also let the distance she covered after noon be,


`d_2`

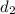
Then,


`39 = (d_2)/(y)`
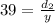
This implies that,


`d_2 = 39y`

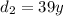
Since she covered a total distance of 238 miles, we can write the equation,

`d_1 + d_2 = 238`

This means that,


`32x + 39y = 238....eqn(2)`



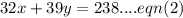
We multiply equation by 32 to get,



`32x + 32y = 224...eqn(3)`


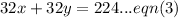
Equation (2) minus equation (3), will give us,


`7y = 14`


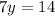
This implies that,

`y = 2`

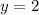
We substitute the value of y into equation (1) to get,


`x + 2 = 7`


`x = 7 - 2`


`x = 5`

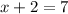
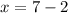
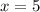
We can now conclude that she averaged at 32 mph for 5 hours and 39 mph for 2 hours.