Answer:

x = 0.76
Explanation:
We can write the area of steel before it is cut as:
Area =
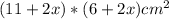
Expanding it by multiplying the brackets to get:
Area =
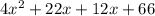
Area area of steel before cutting =
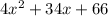
Then we need the area of steel after 11*6 inside dimensions are cut out:
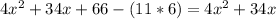
This area should be close to 28 cm
 , hence the equation becomes:
, hence the equation becomes:

Moreover, plotting the graph gives us a value of x = 0.76.