Question

Simplify f+g / f-g when f(x)= x-6 / x+7 and g(x)= x-7 / x+6

Answer 1

C. 2x^2 - 85 / 13

Answer 2

ANSWER


`(f + g)/(f - g) = \frac{2 {x}^(2) - 85 }{ 13}`

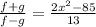
Step-by-step explanation

The given functions are


`f(x) = (x - 6)/(x + 7)`

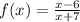
and


`g(x) = (x - 7)/(x + 6)`

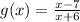
We are required to simplify,


`(f + g)/(f - g)`

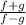
We proceed as follows:


`(f + g)/(f - g) = (f (x)+ g(x))/(f(x) - g(x))`


`(f + g)/(f - g) = ( (x - 6)/(x + 7) + (x - 7)/(x + 6))/((x - 6)/(x + 7) - (x - 7)/(x + 6))`

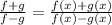
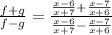
This gives us,


`(f + g)/(f - g) = ( ((x - 6)(x + 6) + (x + 7)(x - 7))/((x + 7)(x + 6)) )/(((x - 6)(x + 6) - (x + 7)(x - 7))/((x + 7)(x + 6)) )`

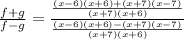
This simplifies to,


`(f + g)/(f - g) = ((x + 6)(x - 6) + (x + 7)(x - 7)/((x - 6)(x + 6) - (x - 7)x + 7))`

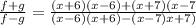
We now apply difference of two squares to get,


`(f + g)/(f - g) = \frac{ {x}^(2) - 36 + {x}^(2) - 49}{ {x}^(2) - 36- ( {x}^(2) - 49)}`


`(f + g)/(f - g) = \frac{ {x}^(2) - 36 + {x}^(2) - 49}{ {x}^(2) - 36- {x}^(2) + 49}`

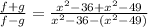
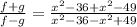
This further simplifies to,


`(f + g)/(f - g) = \frac{2 {x}^(2) - 85 }{ 13}`

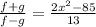
Therefore the correct answer is C