Question

Given: KLMN is a trapezoid, m∠N=m∠KML, FD=8, LM KN = 3/5 F∈ KL , D∈ MN , ME ⊥ KN KF=FL, MD=DN, ME=3root5 Find: KM

Answer 1

The length of KM is
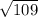`√(109)` units.

Explanation:

Given the statement: KLMN is a trapezoid, ∠N= ∠KML, FD=8,
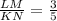`(LM)/(KN)=(3)/(5)`, F∈ KL, D∈ MN , ME ⊥ KN KF=FL, MD=DN,
`ME=3√(5)`.

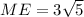From the given information it is noticed that the point F and D are midpoints of KL and MN respectively.

The height of the trapezoid is
`3√(5)`.

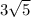Midsegment is a line segment which connects the midpoints of not parallel sides. The length of midsegment of average of parallel lines.

Since
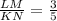`(LM)/(KN)=(3)/(5)`, therefore LM is 3x and KN is 5x.

`(3x+5x)/(2)=8`

`(8x)/(2)=8`

`x=2`

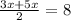
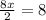
Therefore the length of LM is 6 and length of KN is 10.

Draw perpendicular on KN form L and M.

`KN=KA+AE+EN`

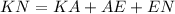
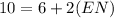`10=6+2(EN)` (KA=EN, isosceles trapezoid)
`EN=2`

`KE=KN-EN=10-2=8`

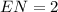
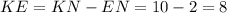
Therefore the length of KE is 8.

Use Pythagoras theorem is triangle EKM.

`Hypotenuse^2=base^2+perpendicular^2`

`(KM)^2=(KE)^2+(ME)^2`

`(KM)^2=(8)^2+(3√(5))^2`

`KM^2=64+9(5)`

`KM=√(109)`

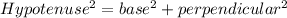
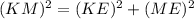
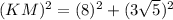
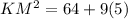
Therefore the length of KM is
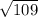`√(109)` units.