Question

Which equation has exactly two real and two non real solutions?

Answer 1

A. x^4 - 21x^2 - 100 = 0

Answer 2

The first option
`x^4-21x^2-100=0`.

Explanation:

To have exactly 2 real and two non real solutions, the degree of the polynomial must be a degree 4. Degree is the highest exponent value in the polynomial and is also the number of solutions to the polynomial. This polynomial ha 2 real+2 non real= 4 solutions and must be
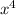`x^4`. This eliminates the bottom two solutions.

In order to have two real and two non real solutions, the polynomial must factor. If it factors all the way like

`x^4-100x^2=0\\x^2(x^2-100)=0\\x^2(x-10)(x+10)=0\\\\x^2=0\\x-10=0\\x+10=0`

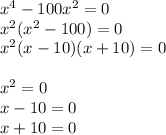
This means x=0, 10, -10 are real solutions to the polynomial. It has no non real solutions. This eliminates this answer choice.

Only answer choice 1 meets the requirement.