Answer:
![f(x)=\sqrt[n]{5x}-10](https://img.qammunity.org/2019/formulas/mathematics/high-school/2jzcpsmwr14s240nzc2qjxzwigpkkrdu89.png)
Explanation:
- Compression of a function (in graph) occurs when the coefficient of the function (the number in front of
 ) increases from 1. e.g. 2, 3, 4, 5 etc.
) increases from 1. e.g. 2, 3, 4, 5 etc. - Expansion is when this same value is a fraction, e.g.
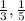 etc.
etc. - Vertical shift upwards is when there is a positive number added to the original function and vertical shift downwards is when there is a negative number added to the original function.
Parent root function is given by:
![f(x)=\sqrt[n]{x}](https://img.qammunity.org/2019/formulas/mathematics/high-school/c4nwnx2lgyvc742lwutbdjach3ob07v0qw.png)
According to rules,
- Compression would be achieved by multiplying the
 by 5. So, we would have
by 5. So, we would have
![\sqrt[n]{5x}](https://img.qammunity.org/2019/formulas/mathematics/high-school/702mzxiynb6vkhs0bq0nrbe44ga8m7m84b.png)
- Downward vertical shift would be achieved by adding a
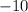 to the function.So,
to the function.So,
![\sqrt[n]{x}-10](https://img.qammunity.org/2019/formulas/mathematics/high-school/s02c29yxuw8nv73e0d2j1bjgl0kzucnrlf.png)
Combining these 2 transformation gives us the function:
![f(x)=\sqrt[n]{5x} -10](https://img.qammunity.org/2019/formulas/mathematics/high-school/b7c1a5h8nu6bx5bzcslvnnb24mvt95arda.png)
Answer choice A is right.