Question

For the first 30 km, the bicyclist rode with a speed of v km/hour. For the remaining 17 km he rode with a speed which was 2 km/hour greater than his original speed. How much time did the bicyclist spend on the entire trip? Let t be the time (in hours), and find t if: v=18

Answer 1

2 hours 31 minutes

Explanation:

Answer 2

t= 2.52 hours

Explanation:

It is given that for first 30 km, the speed of bicyclist is v km/hour

time taken to cover first 30 km is given by

`t_(1) =(30)/(v)` (
`time=(distance)/(speed)`)

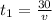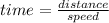for next 17 km the speed of bicyclist is 2 km/hour greater than his original speed

so the speed to cover next 17 km = v+2

time taken to cover next 17 km is given by

`t_(2) =(17)/(v+2)`

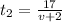
now total time t spent by the bicyclist to cover entire trip is given by

`t=t_(1) +t_(2)`

`t=(30)/(v) +(17)/(v+2)`

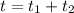
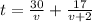
now if v=18 , we have

`t=(30)/(18) +(17)/(20)`

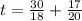
now to add fractions we make the denominator same

Hence we will find the LCM of 18 and 20

LCM of 18 and 20 = 180

now we need to make both the denominator equal to 180

`t=(30(10))/(18(10)) +(17(9))/(20(9))`
`t=(300)/(180) +(153)/(180) =(300+153)/(180)`

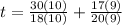
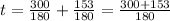
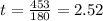`t=(453)/(180) =2.52` hours (approx)