Answer:
Proportion states that the two ratio or fractions are equal.
Given the statement: One grain of sand approximately weighs 7 * 10^{-5} g.
To find how many grains of sand are there in 6300 kg of sand.
Let x be the number of grains of sand in 6300 kg of sand.
Using conversion :
1 kg = 1000 g
6300 kg = 6300000 g
Then, by using proportion method, we have;
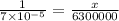
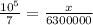
By cross multiply we get;

or

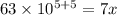 [using
[using
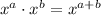 ]
]

Divide both sides by 7 we get;
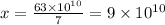
Standard form is a way of of writing down very large or very small numbers easily.
Therefore,
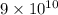 grains of sand are there in 6300 kg of sand.
grains of sand are there in 6300 kg of sand.