Question

A ball is thrown vertically upward from the top of a

building 96 feet tall with an initial velocity of 80 feet
per second. The distance, s (in feet), of the ball from
the ground after t seconds is given by the function:
() = 96 + 80 − 16
2

a. How long does it take for the ball to reach its
highest point?
b. What is the maximum height the ball reaches?

Answer 1

It takes 2.5 seconds for the ball to reach its highest point

Maximum height is 196 feet

Explanation:

h(t) = -16t^2+80t +96

a=-16, b= 80, c=96

To find the maximum height , we need to find vertex

Let find x coordinate of vertex

`t=(-b)/(2a)`

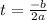
Plug in the values

`t=(-80)/(2(-16))= 2.5`

It takes 2.5 seconds for the ball to reach its highest point

Now plug in 2.5 for t to find maximum height

`h(t) = -16t^2+80t +96`

`h(2.5) = -16(2.5)^2+80(2.5) +96=196`

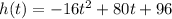
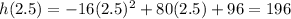
Maximum height is 196 feet