Question

PLEASE HELP ME: if the equation of the regression line for the data set (3,6),(6,2),(9,10) is y=2/3x+2, what is the SSE for the data set?

Answer 1

(3,6) < Pick 2 set's to find the slope
(6,2)

6-2=4
3-6=-3

Slope:-4/3

y=mx+b
6=-4/3(3)+b. <use one of the set's and the...
-4 -4 < inverse
2=b
Y-int = 2
x y
Answer: (-4/3, 2)

Answer 2

The SSE for the data set is: 24

Explanation:

The data points are given by:

(3,6),(6,2),(9,10)

The data points are as follows:

when x=3 y=6

when x=6 y=2

and when x=9 y=10

Also, the line of best fit is as follows:

`y=(2)/(3)x+2`

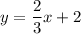
The SSE( sum of square for error ) is calculated as follows:

• Firstly we find the y-values from the line of best fit corresponding to x-values as in the data points.

• Now we find the residual corresponding to each x.

• ( i.e. difference between the actual y-value and y-value on the line of best fit)

• Square this difference quantities and add them up to get SSE of the data set.

• The y-values from the line of best fit

when x=3

from the line of best fit we have: y=4

when x=6

then y=6

when x=9

then y=8

• Hence, the residual value is:

when x=3 6-4= -2

when x=6 2-6= -4

and when x=9 10-8=2

Hence, the square of these difference quantity is:

(-2)²=4

(-4)²=16

and (2)²=4

Hence, the sum of these square quantity is: 4+16+4=24

Hence, the SSE of data is: 24