Question

In trapezoid ABCD with bases AB and DC , diagonals intersect at point O. Find the length of diagonal BD , if BO=6 cm and: AO/OC = 3/1

Answer 1

Explanation:

The ratios of the sides is the same.

3OD=OB

Let y be the length of OD

Therefore,

3y=6

y=2,

meaning OD is 2.

OB+OD=DB

BD=6

ANSWER:

BD=8

Answer 2

BD = 8 cm

Explanation:

Diagonals of trapezoid divides each other in equal ratio.

if ABCD is a trapezoid and the diagonals AC and BD intersect at point O

then we have

`(AO)/(OC) =(OB)/(OD)`

it is given that

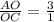`(AO)/(OC) =(3)/(1)` and BO=6 cm

so we can write

`(3)/(1) =(6)/(OD)`

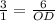
cross multiply

`3 OD=6`

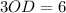
divide both side by 3

OD= 2 cm

now we have

BD = BO +OC

BD = 6 cm + 2 cm

BD= 8 cm