Question

The coordinates of the vertices of JKL are J(-5, -1), K(0, 1) , and L(2, -5). Which statement correctly describes whether JKL is a right triangle?

Answer 1

It is NOT a right triangle.

Explanation:

You must figure out the slopes of the segments of the triangle to see if it is a right triangle. If they are perpendicular (meaning the slopes are negative reciprocals of each other), they form a right angle, making it a right triangle.

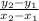`(y_(2) -y_(1))/(x_(2) -x_(1))` This formula finds slope using two points.

Let's figure out the slope of JK.

(-1-1)/(-5-0) = m

Simplify.

-2/-5 = m

A negative divided by a negative makes a positive.

2/5 = m

Now LK.

(-5-1)/(2-0) = m

Simplify.

-6/2 = m

Divide.

-3/1 = m

Now JL.

(-1+5)/(-5-2) = m

Simplify.

4/-3 = m

None of these slopes are negative reciprocals of each other, thus deeming it not a right triangle.